第四讲 测量准确度、重复性、复现性及标准偏差(3)

对同一被测量做有限的n次测量，其中任何一次的测量结果或观测值，都可视作无穷多次测量结果或总体的一个样本。数理统计方法就是要通过这个样本所获得的信息(例如算术平均值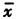和实验标准差s等)，来推断总体的性质(例如期望μ和方差σ2等)。定义注1中指出:当将n个值视作分布的取样时,x为该分大上的期望的无偏差估计,s2为该分布的方差σ2的无偏差估计。其中期望是通过无穷多次测量所得的观测值的算术平均值或加权平均值，又称为总体均值μ。显然，它只是在理论上存在并可表示为    μ=Lim  ∑xi    注1所说的方差σ2，则是无穷多次测量所得观测值xi与期望μ之差的平方的算术平均值，它也只是在理论上存在并可表示为
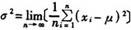方差的正平方根σ，通常被称为标准〔偏〕差，又称为总体标准〔偏〕差(population standard deviation)或理论标准〔偏〕差，而本定义中通过有限次测量求得的实验标准〔偏〕差s，又称为样本标准〔偏〕差(sample standard deviation)。s是σ的估计值。

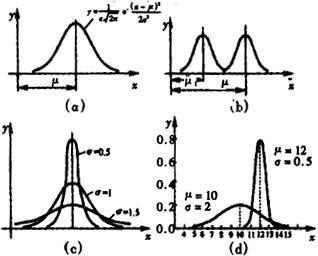
正态分布的总体均值和总体标准[偏]差
　　图中示出了总体均值为μ，总体标准〔偏〕差为σ的正态分布的情形。由图(c)可见，σ愈小，分布曲线愈集中或愈尖锐，表征测量结果或观测值的分散性愈小；反之σ愈大，曲线愈平坦，表征分散性愈大。由图(a)可见，分布曲线在x=μ处具有极大值，曲线不仅是单峰的，而且对x=μ直线来说是对称的，在x=μ±σ处有两个拐点。由图(b)可见，分布的中心在x-μ处，μ值的大小决定了曲线在x轴上的位置，图(d)对两条不同μ值和不同σ值的正态分布曲线进行了比较。
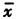　　为μ的无偏估计，s2为σ2的无偏估计。这里的“无偏估计”可理解为: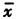比μ大的概率，与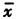比μ小的概率是相等的或皆为50%；而且当n→∞时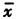，(-μ)→0。值得注意的是:s2为σ2的无偏估计，但s不是σ的无偏估计，而是偏小估计，即(s-σ)为负值的概率，大于(s-σ)为正值的概率。　　 s是单次观测值xi的实验标准〔偏〕差，
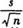才是n次测量所得算术平均值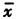的实验标准〔偏〕差，它是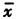分布的标准〔偏〕差的估计值。为易于区别，前者用s(x)表示，后者用s(
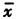)表示，故有s( 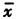)=s(x)/√n。

通常用s(x)表征测量仪器的重复性，而用s(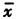)评价从此仪器进行n次测量所得测量结果的分散性。随着测量次数n的增加，测量结果的分散性s(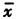)即与√n

成反比地减小，这是由于对多次观测值取平均后，正、负误差相互抵偿所致。所以，当测量要求较高或希望测量结果的标准〔偏差〕较小时，应适当增加n；但是n>20时，随着n的增加，s(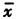)的减少速率减慢。因此，在选取n的多少时应予综合考虑或权衡利弊，因为增加测量次数就会拉长测量时间、加大测量成本。在通常情况下，取n≥3，以n=4～20为宜。　　应当强调的是:s(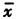)是平均值的实验标准〔偏〕差，而不能称它为平均值的标准误差。