服务科学|服务科学研究|服务生产|服务社会各业
服务热线
010 53561328 (总机)/15712870585/010 62423361/010 62423562
晶体学资料室
服务查询


通用计量术语知识讲座
第四讲 测量准确度、重复性、复现性及标准偏差(2)
编辑:本站 点击: 来源:网上搜集 发布时间:2014年01月15日
二、[测量结果的]重复性 是指“在相同测量条件下,对同一被测量进行连续多次测量所得结果之间的一致性”(5.6条)。 上述定义中的“一致性”是定量的,可以用重复性条件下对同一量进行多次测量所得结果的分散性来表示。而表示测量结果分散性的量,最为常用的是实验标准〔偏〕差(见5.8条)。在重复性条件下按贝塞尔(Bessel)公式算得的实验标准〔偏〕差被称为“重复性标准差”,并记以sr。下标r被称为“重复性限”,它是重复性条件下两次测量结果之差以95%的概率所存在的区间,即两次测量结果之差落于r这个区间内或这个差≤r的概率为95%。假定多次测量所得结果呈正态分布,而且算得的sr充分可靠(自由度充分大),则可求得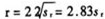 ,即重复性限约为重复性标准差的3倍。观测者通常可以利用重复性限,来了解测量方法导致的不确定度(见5.9条),并用于评定测量结果是否符合要求。 重复性条件包括注2中所列的五个内容。质言之,就是在尽量相同的条件下,包括程序、人员、仪器、环境等,以及尽量短的时间间隔内完成重复测量任务。这里的“短时间”可理解为:保证前四个条件相同或保持不变的时间段,它主要取决于人员的素质、仪器的性能以及对各种影响量(见4.8条)的监控。从数理统计和数据处理的角度来看,在这段时间内测量应处于统计控制状态,即符合统计规律的随机状态。通俗地说,它是测量处于正常状态的时间间隔。重复观测中的变动性,正是由于各种影响量不能完全保持恒定而引起的。重复性标准差有时也称为组内标准差。
,即重复性限约为重复性标准差的3倍。观测者通常可以利用重复性限,来了解测量方法导致的不确定度(见5.9条),并用于评定测量结果是否符合要求。 重复性条件包括注2中所列的五个内容。质言之,就是在尽量相同的条件下,包括程序、人员、仪器、环境等,以及尽量短的时间间隔内完成重复测量任务。这里的“短时间”可理解为:保证前四个条件相同或保持不变的时间段,它主要取决于人员的素质、仪器的性能以及对各种影响量(见4.8条)的监控。从数理统计和数据处理的角度来看,在这段时间内测量应处于统计控制状态,即符合统计规律的随机状态。通俗地说,它是测量处于正常状态的时间间隔。重复观测中的变动性,正是由于各种影响量不能完全保持恒定而引起的。重复性标准差有时也称为组内标准差。
三、[测量结果的]复现性 是指“在改变了的测量条件下,同一被测量的测量结果之间的一致性”(5.7条)。 上述定义的“一致性”是定量的,可以用复现性条件下对同一量进行重复测量所得结果的分散性来表示。这个表示测量结果分散性的量,通常按贝塞尔公式算得,被称为“复现性标准差”并记以sr。下标r被称为“复现性限”,其含义类似于5.6条中的重复性限。假定复现性条件是两个地点的不同实验室,则观测者可以利用复现性限,来验证这两个实验室之间是否存在过大的系统效应而导致的不确定度。 复现性条件包括注2中所列的八个内容。这些内容可以改变其中一项、多项或全部。因此,在复现性的有效表述中,应说明变化条件(复现性条件)的规范。例如:在进行校准实验室比对或能力验证试验时,主导实验室将一块三等标准砝码逐次送往若干个参加实验室,要求各室按三等标准砝码检定规范规定的方法进行测量。这里,测量原理、测量方法、使用条件没有改变,但观测者、测量仪器(天平)、参考测量标准(二等标准砝码)、地点、时间均发生了改变。 这时对各室得到的测量结果,首先应按各自所用的参考测量标准的修正值进行相应地修正,然后再按贝塞尔公式计算出sr。此即注4所说的“测量结果在这里通常理解为已修正结果”。假定按5.6条在重复性条件下进行若干次测量,由于在同一个实验室使用的是同一个参考测量标准(同一块二等标准砝码),因而在计算sr时就没有必要按参考测量标准的修正值进行修正。复现性又称为再现性。复现性标准差有时也称为组间标准差。
四、实验标准[偏]差 是指“对同一被测量做n次测量,表征测量结果分散性的量s可按下式算出: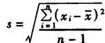 式中:xi为第i次测量的结果;
式中:xi为第i次测量的结果;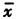 为所考虑的n次测量结果的算术平均值”(5.8
为所考虑的n次测量结果的算术平均值”(5.8
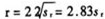 ,即重复性限约为重复性标准差的3倍。观测者通常可以利用重复性限,来了解测量方法导致的不确定度(见5.9条),并用于评定测量结果是否符合要求。 重复性条件包括注2中所列的五个内容。质言之,就是在尽量相同的条件下,包括程序、人员、仪器、环境等,以及尽量短的时间间隔内完成重复测量任务。这里的“短时间”可理解为:保证前四个条件相同或保持不变的时间段,它主要取决于人员的素质、仪器的性能以及对各种影响量(见4.8条)的监控。从数理统计和数据处理的角度来看,在这段时间内测量应处于统计控制状态,即符合统计规律的随机状态。通俗地说,它是测量处于正常状态的时间间隔。重复观测中的变动性,正是由于各种影响量不能完全保持恒定而引起的。重复性标准差有时也称为组内标准差。
,即重复性限约为重复性标准差的3倍。观测者通常可以利用重复性限,来了解测量方法导致的不确定度(见5.9条),并用于评定测量结果是否符合要求。 重复性条件包括注2中所列的五个内容。质言之,就是在尽量相同的条件下,包括程序、人员、仪器、环境等,以及尽量短的时间间隔内完成重复测量任务。这里的“短时间”可理解为:保证前四个条件相同或保持不变的时间段,它主要取决于人员的素质、仪器的性能以及对各种影响量(见4.8条)的监控。从数理统计和数据处理的角度来看,在这段时间内测量应处于统计控制状态,即符合统计规律的随机状态。通俗地说,它是测量处于正常状态的时间间隔。重复观测中的变动性,正是由于各种影响量不能完全保持恒定而引起的。重复性标准差有时也称为组内标准差。三、[测量结果的]复现性 是指“在改变了的测量条件下,同一被测量的测量结果之间的一致性”(5.7条)。 上述定义的“一致性”是定量的,可以用复现性条件下对同一量进行重复测量所得结果的分散性来表示。这个表示测量结果分散性的量,通常按贝塞尔公式算得,被称为“复现性标准差”并记以sr。下标r被称为“复现性限”,其含义类似于5.6条中的重复性限。假定复现性条件是两个地点的不同实验室,则观测者可以利用复现性限,来验证这两个实验室之间是否存在过大的系统效应而导致的不确定度。 复现性条件包括注2中所列的八个内容。这些内容可以改变其中一项、多项或全部。因此,在复现性的有效表述中,应说明变化条件(复现性条件)的规范。例如:在进行校准实验室比对或能力验证试验时,主导实验室将一块三等标准砝码逐次送往若干个参加实验室,要求各室按三等标准砝码检定规范规定的方法进行测量。这里,测量原理、测量方法、使用条件没有改变,但观测者、测量仪器(天平)、参考测量标准(二等标准砝码)、地点、时间均发生了改变。 这时对各室得到的测量结果,首先应按各自所用的参考测量标准的修正值进行相应地修正,然后再按贝塞尔公式计算出sr。此即注4所说的“测量结果在这里通常理解为已修正结果”。假定按5.6条在重复性条件下进行若干次测量,由于在同一个实验室使用的是同一个参考测量标准(同一块二等标准砝码),因而在计算sr时就没有必要按参考测量标准的修正值进行修正。复现性又称为再现性。复现性标准差有时也称为组间标准差。
四、实验标准[偏]差 是指“对同一被测量做n次测量,表征测量结果分散性的量s可按下式算出:
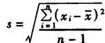 式中:xi为第i次测量的结果;
式中:xi为第i次测量的结果;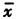 为所考虑的n次测量结果的算术平均值”(5.8
为所考虑的n次测量结果的算术平均值”(5.8